Comment Savoir Si C'est Un Triangle Rectangle

Un article de Wikipédia, l'encyclopédie libre.

Représentation d'un triangle ABC rectangle en C.

En géométrie euclidienne, un triangle rectangle est un triangle dont l'united nations des angles est droit. Les deux autres angles sont alors complémentaires, de mesure strictement inférieure^[i]. On nomme alors hypoténuse le côté opposé à 50'angle droit. Les deux autres côtés, adjacents à l'angle droit, sont appelés cathètes.

Fifty'hypoténuse est alors le plus g côté du triangle, et sa longueur est reliée à celles des deux autres côtés par le théorème de Pythagore. Cette relation est même caractéristique des triangles rectangles. Dans le cas des triangles à côtés entiers, elle mène à la définition des triplets pythagoriciens.

Propriétés caractéristiques [modifier | modifier le lawmaking]

Théorème de Pythagore [modifier | modifier le code]

Le théorème de Pythagore précise que dans united nations triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des deux autres longueurs des côtés de l'bending droit, autrement dit, si un triangle ABC est rectangle en C, alors $AB^{2}=CA^{2}+CB^{two}$ .

Réciproquement, tout triangle ABC vérifiant l'égalité précédente est un triangle rectangle en C.

Aire [modifier | modifier le code]

Comme united nations triangle rectangle peut se réaliser comme la moitié d'un rectangle engendré par les deux cathètes, l'aire d'un triangle rectangle est égale à la moitié du produit des longueurs de ces deux côtés.

Récriproquement, si l'aire d'un triangle est le produit des longueurs de deux côtés divisé par 2, alors ce triangle est rectangle au sommet commun à ces côtés.

Cercle circonscrit [modifier | modifier le code]

Médiane de l'angle droit d'un triangle rectangle

Si un triangle est rectangle, alors le milieu de l'hypoténuse est à égale distance des trois sommets, c'est-à-dire qu'il est le middle du cercle circonscrit, ou encore que la médiane outcome de l'angle droit a pour longueur la moitié de l'hypoténuse^[2].

Réciproquement, tout signal d'un cercle forme un triangle rectangle avec les extrémités d'united nations diamètre de ce cercle.

Cette équivalence peut être vue comme un cas particulier du théorème de fifty'angle au heart : fifty'angle inscrit est droit si et seulement si l'bending au middle est plat.

Hauteurs [modifier | modifier le lawmaking]

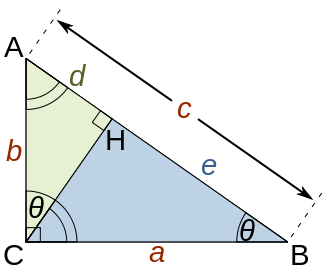
Triangle rectangle et pied de la hauteur

La hauteur issue de l'bending droit d'un triangle rectangle possède des propriétés caractéristiques dont 50'une apparaît dans les premières pages du livre de René Descartes, La géométrie.

Dans tout triangle ABC dont H est le pied de la hauteur issue de C.

Si le triangle est rectangle en C alors^[3] :
- H appartient à [AB] et CH^two = HA × HB ;
- H appartient à [AB] et Ac^two = AH × AB ;
- H appartient à [AB] et BCⁱⁱ = BH × AB ;
- CH × AB = CA × CB.
Réciproquement, un triangle dans lequel l'une de ces quatre propriétés est réalisée est rectangle en C.

Les trois premières propriétés se déduisent de l'ascertainment des trois triangles semblables ABC, CBH et ACH. La quatrième consiste à écrire fifty'aire du triangle rectangle en considérant successivement BC et BA comme base.

Les réciproques utilisent les mêmes outils : les premières égalités traduisent des égalités de rapports et la présence d'united nations bending droit ou d'un bending en commun confirment la présence de triangles semblables, qui sont donc rectangles.

L'orthocentre d'united nations triangle rectangle est de manière évidente le sommet où se trouve l'angle droit.

Dans un triangle rectangle, la hauteur issue de l'angle droit, a une longueur HC égale à la somme des rayons des cercles inscrits respectivement dans le triangle rectangle initial ABC et les deux triangles rectangles délimités par la hauteur. Si on appelle $r$ le rayon du cercle inscrit dans le triangle ABC, $r 1$ celui du cercle inscrit dans le triangle AHC, $r 2$ celui du cercle inscrit dans le triangle BHC, et $h$ la hauteur CH, on a :

h=r+r_{i}+r_{2}

La hauteur $h$ , les rayons $r$ , $r 1$ et $r 2$ sont liés par les relations : ${\frac {h}{r_{1}}}={\frac {a}{r}}$ et ${\frac {h}{r_{2}}}={\frac {b}{r}}$

r^{ii}=r_{1}^{2}+r_{2}^{2}

{\frac {r_{1}}{b}}={\frac {r_{two}}{a}}={\frac {r}{c}}

Bissectrice [modifier | modifier le code]

Triangle rectangle et son cercle inscrit

Dans tout triangle rectangle, les bissectrices se rencontrent en united nations point O centre du cercle inscrit au triangle. Le rayon de ce cercle inscrit est égal au demi-périmètre moins l'hypoténuse (voir schéma) soit, avec les mêmes notations :

$r = AB + BC + CA / 2 - AB$ .

On retrouve le théorème de Carnot, qui appliqué au triangle rectangle en C, donne, r étant le rayon du cercle inscrit, et R = AB / 2 celui du cercle circonscrit :

$CA + CB / 2$ = r + R et $CA + CB = AB + 2 r$

Le rayon r du cercle inscrit est aussi égal à deux fois la surface du triangle divisée par le périmètre.

Cas particuliers [modifier | modifier le lawmaking]

Ces triangles sont uniques à similitude près.

Triangle isocèle rectangle [modifier | modifier le code]

Le demi-carré est un triangle isocèle rectangle. Ses deux angles aigus mesurent 45°, et le rapport entre son hypoténuse et chacune de ses cathètes vaut √2 .

Triangle 3-four-five [modifier | modifier le code]

Le triangle 3-4-5 est un triangle dont les côtés mesurent respectivement 3, iv et five unités. Il southward'agit du triangle rectangle à côtés entiers avec 50'hypoténuse minimale, et le seul triangle dont les longueurs de côtés suivent une progression arithmétique. Cette forme est mise à profit pour obtenir united nations angle droit à fifty'adjutant de la corde à xiii nœuds.

Triangle de Kepler [modifier | modifier le code]

Le triangle de Kepler est le seul triangle rectangle dont les longueurs de côtés suivent une progression géométrique. La raison de cette progression est la racine carrée du nombre d'or.

Demi-triangle équilatéral [modifier | modifier le code]

Le demi-triangle équilatéral a cascade angles ninety°, lx° et 30°. C'est le seul triangle rectangle dont les angles suivent une progression arithmétique.

Applications [modifier | modifier le code]

Décomposition [modifier | modifier le lawmaking]

Tout triangle non plat peut être décomposé en deux triangles rectangles admettant cascade côté commun une hauteur interne (par exemple, celle event d'united nations sommet d'angle maximal).

Ce principe permet de ramener les problèmes de pavages par des polygones à des problèmes de pavage par des triangles rectangles.

Composantes dans un repère orthonormé [modifier | modifier le code]

Dans un repère orthonormé $(O,{\vec {\imath }},{\vec {\jmath }})$ , si un betoken M se projette selon H sur l'axe $(O,{\vec {\imath }})$ et selon I sur l'axe $(O,{\vec {\jmath }})$ , alors OHM et OMI sont des triangles rectangles.

Trigonométrie dans le triangle rectangle [modifier | modifier le lawmaking]

$\scriptstyle \cos \alpha =\sin \beta ={\frac {Air conditioning}{AB}},\ \scriptstyle \sin \alpha =\cos \beta ={\frac {BC}{AB}}$

Un triangle rectangle comporte un angle droit et deux angles aigus, du moins en géométrie euclidienne (sur une sphère, il existe des triangles à deux et même trois angles droits).

Deux triangles rectangles ayant un de leurs angles not droits égaux sont semblables : le rapport de deux des côtés du triangle rectangle ne dépend donc que d'un angle non droit. Cette propriété permet d'introduire les fonctions trigonométriques cascade un bending aigu non orienté, dont la mesure est, en degré entre 0 et 90° (ou en radians, entre 0 et π/two). Par exemple pour united nations triangle ABC rectangle en C :

le cosinus de l'angle α est le rapport du côté de 50'bending droit adjacent à α par l'hypoténuse, soit cos(α) = Air-conditioning/AB ;
le sinus de fifty'bending α est le rapport du côté de l'angle droit opposé à α par l'hypoténuse, soit sin(α) = BC/AB ;
la tangente de l'bending α est le rapport du côté de l'angle droit opposé à α par côté de l'angle droit next à α, tan(α) = BC/Ac.

Triangle pythagoricien [modifier | modifier le code]

Le triangle 3-four-v, un exemple bien connu de triangle rectangle pythagoricien

Un triangle rectangle dont les trois côtés sont mesurés par des nombres entiers (cascade une même unité de mesure) est appelé triangle pythagoricien. Par le théorème de Pythagore, les longueurs des trois côtés d'united nations triangle pythagoricien fournissent united nations triplet pythagoricien, qui est united nations triplet de nombres entiers (10, y, z) non nuls vérifiant x ² + y ² = z ². Par la réciproque du même théorème, un triplet pythagoricien permet de construire united nations triangle pythagoricien.

En particulier pour tout nombre entier n supérieur ou égal à 3, on peut construire united nations triangle rectangle dont la longueur d'un côté de fifty'bending droit est mesurée par ce nombre n, les deux autres côtés étant mesurés par des nombres entiers :

Si due north est un nombre pair, northward = twok, il suffit de prendre la longueur de 50'autre côté de l'bending droit égale à chiliad ² - 1. L'hypoténuse est alors de longueur égale à k ²+one.
Si n est united nations nombre impair, northward = two1000 + 1, il suffit de prendre la longueur de l'autre côté de l'bending droit égale à twok ² + iik. L'hypoténuse est alors de longueur égale à twochiliad ² + twog + 1.

On sait décrire plus généralement tous les triplets, et donc tous les triangles, pythagoriciens. Fermat a démontré qu'aucun de ceux-ci ne pouvait avoir pour aire un carré parfait.

Spirale de Théodore [modifier | modifier le code]

La spirale de Théodore est constituée d'une suite de triangles rectangles, chacun admettant une cathète de longueur ane et l'autre définie par 50'hypoténuse du triangle précédent. Le triangle initial est isocèle rectangle. La suite des longueurs des hypoténuses est constituée des racines carrées des entiers naturels. Cette spirale est nommée en hommage à Théodore de Cyrène qui aurait démontré que les racines carrées des premiers entiers (hors carrés parfaits) étaient irrationnelles.

Généralisations [modifier | modifier le code]

Tétraèdre trirectangle [modifier | modifier le code]

Un tétraèdre est dit trirectangle si trois de ses faces sont des triangles rectangles en un même sommet. Le théorème de de Gua généralise alors le théorème de Pythagore en stipulant que le carré de l'aire de la dernière face up est la somme des carrés des aires des trois autres.

Triangle rectangle sphérique [modifier | modifier le code]

Représentation d'un triangle trirectangle.

En géométrie non euclidienne, un triangle rectangle sphérique peut posséder deux ou trois angles droits^[iv].

Notes et références [modifier | modifier le code]

↑ Si on exclut la possibilité que deux sommets soient confondus, united nations triangle ne peut admettre deux angles droits et un bending nul.
↑ propriété caractéristique parfois attribuée à Thalès.
↑ «Les relations métriques dans le triangle rectangle », sur alloprof.qc.ca .
↑ Joseph Casimir Pascal, Cours de géométrie élémentaire, Bachelier, 1835, 367p. (lire en ligne) .

Voir aussi [modifier | modifier le code]

Triangle acutangle
Triangle obtusangle
Triangle rectangle spécial(en)
Tétraèdre trirectangle

Portail de la géométrie